Overview
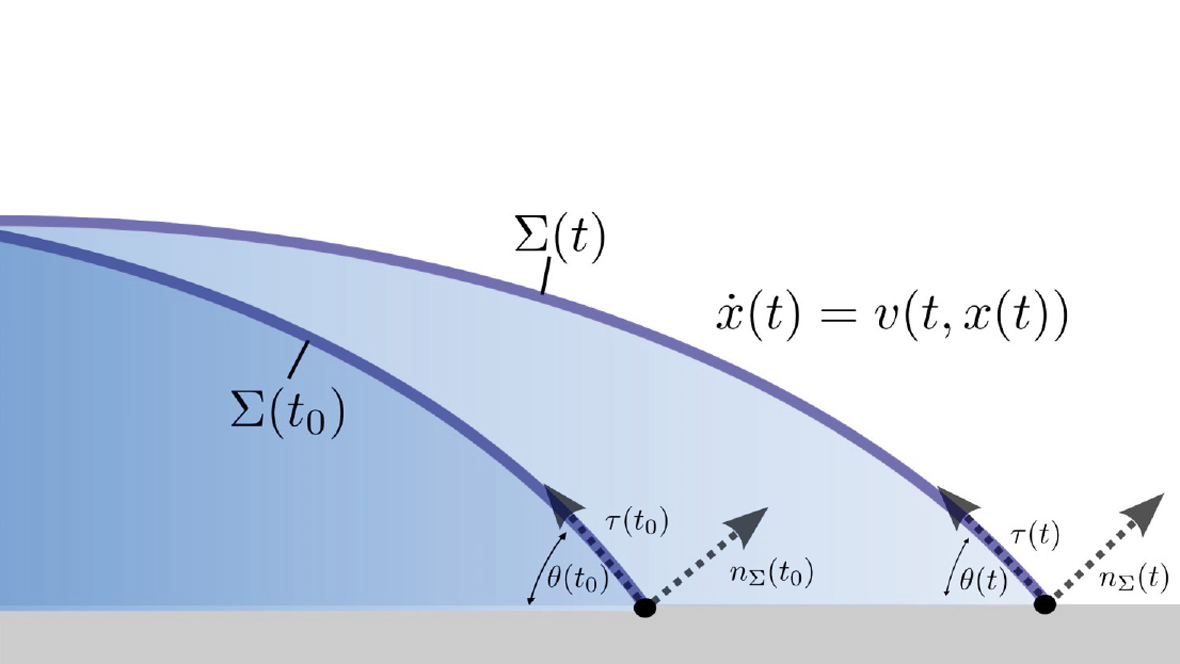
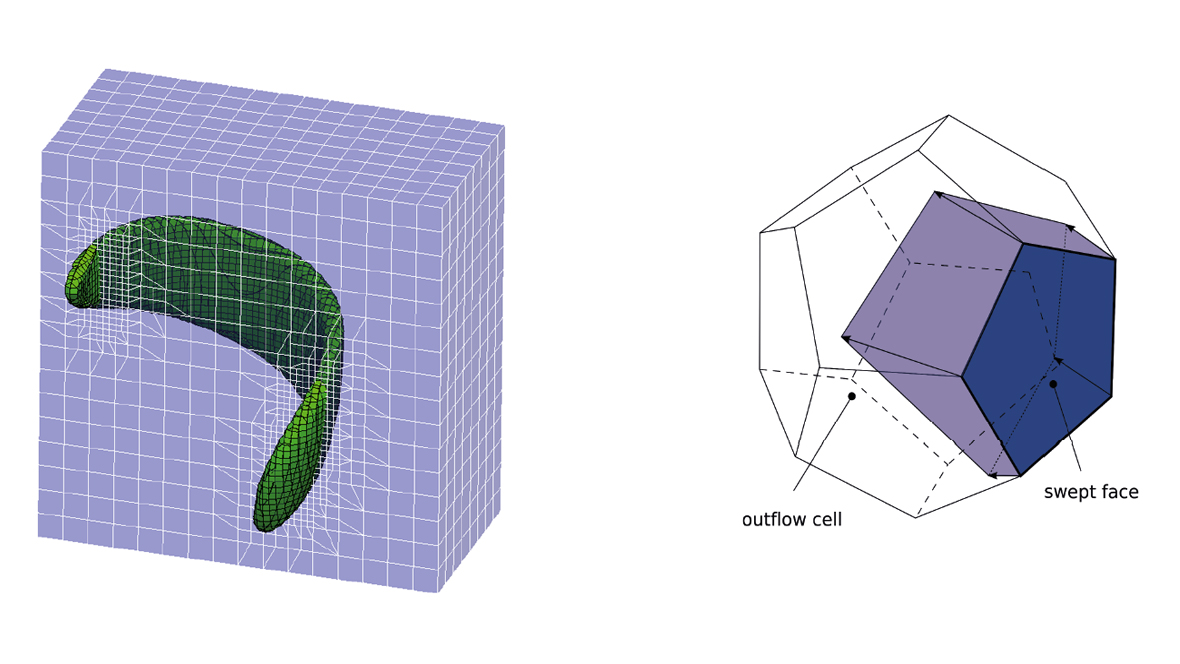
In B01, the fundamental understanding of local processes at dynamic contact lines will be enhanced by rigorous modeling of contact angle hysteresis, dissipation and rolling motion at the contact line. The second focus lies on further development of the geometric Volume of Fluid method. Here the treatment of dynamic contact lines from FS3D has to be transferred to the case of unstructured, dynamically adaptive grids using voFoam in OpenFOAM. Regarding the simulation of, especially, the generic configurations in cooperation with A01, A02 and A05, further numerical developments are planned, for example concerning the wetting of rough surfaces, treatment of pinning and contact angle hysteresis as well as visco-elastic flow behavior.
Team
| Name | Contact | |
|---|---|---|

| Prof. Dr. Dieter Bothe Deputy Speaker, Coordinator Area B | bothe@mma.tu-... +49 6151 16-21463 L2|06 400 |

| Muhammad Hassan Asghar M.Sc. | hassan.asghar@tu-... +49 6151 16-21470 L2|06 412 |
Publications and conference contributions

Error on loading data
An error has occured when loading publications data from TUbiblio. Please try again later.
-
{{ year }}
-
; {{ creator.name.family }}, {{ creator.name.given }}{{ publication.title }}.
; {{ editor.name.family }}, {{ editor.name.given }} (eds.); ; {{ creator }} (Corporate Creator) ({{ publication.date.toString().substring(0,4) }}):
In: {{ publication.series }}, {{ publication.volume }}, In: {{ publication.book_title }}, In: {{ publication.publication }}, {{ publication.journal_volume}} ({{ publication.number }}), ppp. {{ publication.pagerange }}, {{ publication.place_of_pub }}, {{ publication.publisher }}, {{ publication.institution }}, {{ publication.event_title }}, {{ publication.event_location }}, {{ publication.event_dates }}, ISSN {{ publication.issn }}, e-ISSN {{ publication.eissn }}, ISBN {{ publication.isbn }}, DOI: {{ publication.doi.toString().replace('http://','').replace('https://','').replace('dx.doi.org/','').replace('doi.org/','').replace('doi.org','').replace("DOI: ", "").replace("doi:", "") }}, Official URL, {{ labels[publication.type]?labels[publication.type]:publication.type }}, {{ labels[publication.pub_sequence] }}, {{ labels[publication.doc_status] }} - […]
-
Number of items in this list: >{{ publicationsList.length }}
Only the {{publicationsList.length}} latest publications are displayed here.