Überblick
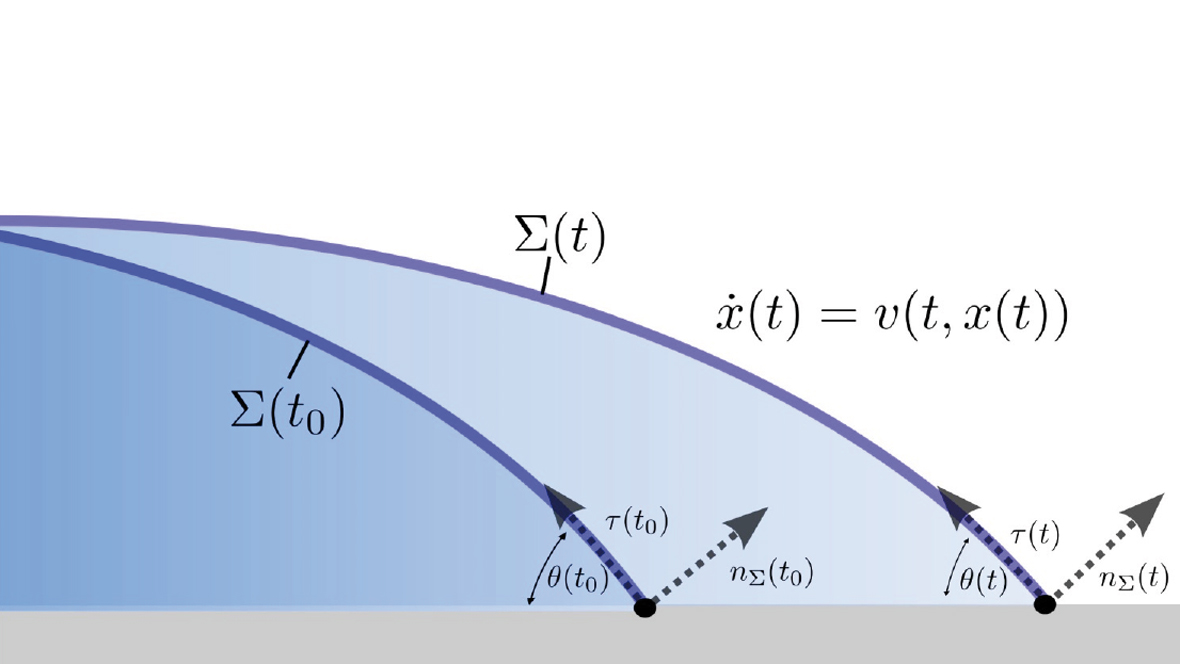
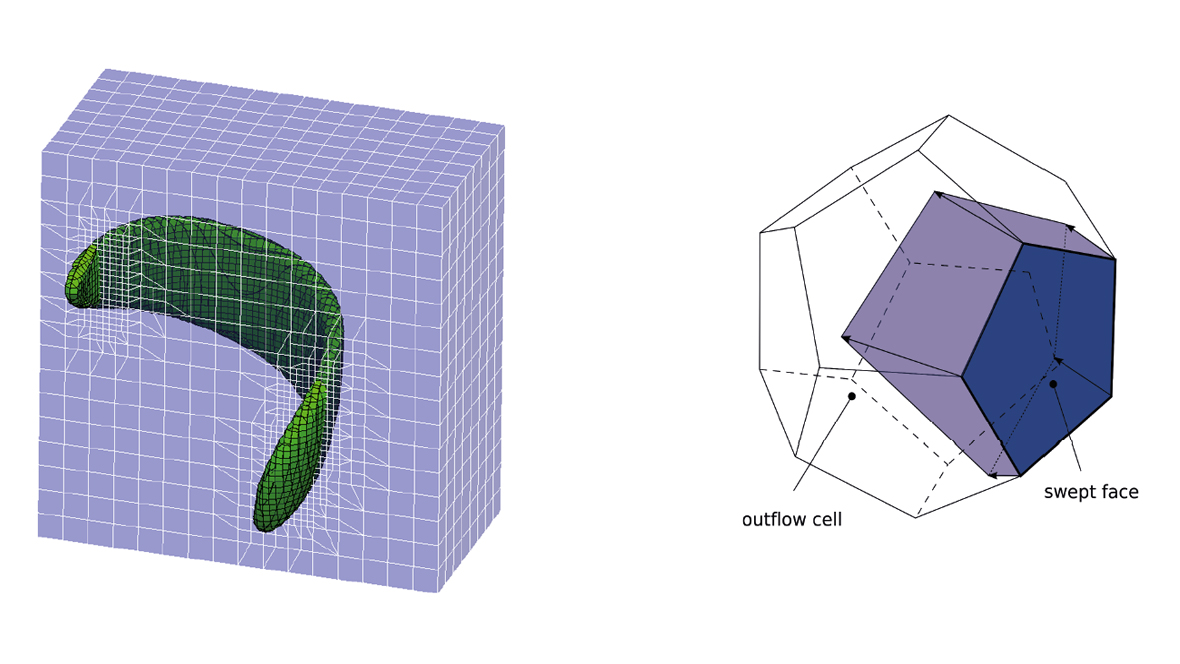
In B01 soll das fundamentale Verständnis lokaler Prozesse an dynamischen Kontaktlinien vertieft werden, indem u.a. Kontaktwinkelhysterese, Dissipation sowie Rollbewegung der Flüssigkeit an der Kontaktlinie rigoros modelliert werden. Zweiter Schwerpunkt ist die Weiterentwicklung der geometrischen Volume of Fluid Methode. Hier ist die Behandlung dynamischer Kontaktlinien aus FS3D auf den Fall unstrukturierter, dynamisch adaptiver Gitter mittels voFoam in OpenFOAM zu übertragen. Zur Simulation v.a. der Leitkonfigurationen in Kooperation mit A01, A02 und A05 sind weitere numerische Entwicklungen geplant, etwa zur Benetzung rauer Oberflächen, Behandlung von Pinning und Kontaktwinkelhysterese sowie viskoelastischem Fließverhalten.
Team
| Name | Kontakt | |
|---|---|---|

| Prof. Dr. Dieter Bothe | bothe@mma.tu-... +49 6151 16-21463 L2|06 400 |

| Muhammad Hassan Asghar M.Sc. | hassan.asghar@tu-... +49 6151 16-21470 L2|06 412 |
Aus dem Teilprojekt entstandene Publikationen und Konferenzbeiträge

Fehler beim Laden der Daten
Beim Laden der Publikationsdaten von TUbiblio ist ein Fehler aufgetreten. Bitte versuchen Sie es zu einem späteren Zeitpunkt erneut.
-
{{ year }}
-
; {{ creator.name.family }}, {{ creator.name.given }}{{ publication.title }}.
; {{ editor.name.family }}, {{ editor.name.given }} (Hrsg.); ; {{ creator }} (Urheber) ({{ publication.date.toString().substring(0,4) }}):
In: {{ publication.series }}, {{ publication.volume }}, In: {{ publication.book_title }}, In: {{ publication.publication }}, {{ publication.journal_volume}} ({{ publication.number }}), SS. {{ publication.pagerange }}, {{ publication.place_of_pub }}, {{ publication.publisher }}, {{ publication.institution }}, {{ publication.event_title }}, {{ publication.event_location }}, {{ publication.event_dates }}, ISSN {{ publication.issn }}, e-ISSN {{ publication.eissn }}, ISBN {{ publication.isbn }}, DOI: {{ publication.doi.toString().replace('http://','').replace('https://','').replace('dx.doi.org/','').replace('doi.org/','').replace('doi.org','').replace("DOI: ", "").replace("doi:", "") }}, Offizielle URL, {{ labels[publication.type]?labels[publication.type]:publication.type }}, {{ labels[publication.pub_sequence] }}, {{ labels[publication.doc_status] }} - […]
-
Anzahl der Einträge in dieser Liste: >{{ publicationsList.length }}
Es werden nur die {{publicationsList.length}} neuesten Publikationen ausgegeben.
Vollständige Liste bei TUbiblio ansehen Diese Liste bei TUbiblio ansehen