Many transport processes in nature and technology can be described mathematically through continuum models. In the language of mathematics these are described by means of partial differential equations (PDE). Of course, analytical solutions are known only in a few exceptional cases and for simple or simplified models. That is why the understanding and, if possible, the improvement of those processes requires a numerical solution of systems of PDEs.
Equation Mimicking
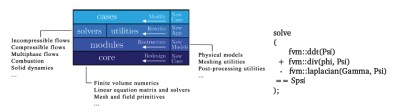
OpenFOAM is not a monolithic software! Its flexible and efficient C++ library accompanied by more than 80 specialized programs (“top-level solvers”) and more than 170 utilities (pre- and post-processing tools) which have to be understood as examples for the use of this library.
OpenFOAM allows the description of data types and basic operations of CCM. The top-level syntax follows the tensor notation (i.e. the mathematical language for PDEs) as closely as possible. This is called ”equation mimmicking“: Differential operators can be directly ”translated" term by term from the mathematical language of the PDEs into valid C++ code. The diffusion or Laplace operator as found in heat transfer problems for instance becomes fvm::laplacian(D, T) in OpenFOAM/C++.
Besides its flexibility and capabilities OpenFOAM code is parallelised per se and as such can be used on supercomputers such as the Lichtenberg High Performance Computer of the TU Darmstadt without further ado.
This flexibility by separating numerical formulation and the solution of the system of model equations often turns simulation-based research of complex processes upside down: OpenFOAM is inherently based upon a modular concept, which allows for flexibility in assembling its methods. This has significant potential for exploring and improving even complex technical transport processes using numerical simulation methods in an efficient manner.
Central platform
Within the CRC great importance is attached to the the open C++ library OpenFOAM. The software considerably supports interdisciplinary cooperation during model development and simulation at different levels of detail. OpenFOAM has been selected as a common, central developmental platform to implement new modelling approaches and simulation methodologies within the CRC.